gdy ułamek „normalny” zawiera ułamki w liczniku lub mianowniku lub w obu, to uważamy, że jest to ułamek złożony. Ten rodzaj frakcji jest również znany jako frakcja złożona.
istnieją dwie metody upraszczające taki rodzaj ułamka.
Metoda 1
kluczowe kroki:
- Utwórz pojedynczy ułamek w liczniku i mianowniku.,
- Zastosuj regułę dzielenia ułamków mnożąc licznik przez odwrotność lub odwrotność mianownika.
Metoda 2
kluczowe kroki:
- Znajdź najmniejszy wspólny mianownik (LCD) wszystkich mianowników w złożonych ułamkach.
- pomnóż ten LCD do licznika i mianownika ułamka złożonego.
- ,
po przejrzeniu kilku przykładów powinieneś zdać sobie sprawę, że Metoda 2 jest znacznie lepsza niż metoda 1, ponieważ prawie zawsze potrzeba mniej kroków, aby uzyskać ostateczną odpowiedź.
przykłady jak uprościć złożone ułamki
przykład 1: uprościć złożone ułamki poniżej.
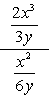
- używając metody 1
zarówno licznik, jak i mianownik ułamka złożonego są już wyrażone jako ułamki pojedyncze. To jest świetne!,

następnym krokiem jest zastosowanie zasady podziału przez pomnożenie licznika przez odwrotność mianownika. Zakończ, anulując wspólne czynniki, aby uzyskać ostateczną odpowiedź.
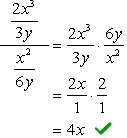
- używając metody 2
Znajdź wyświetlacz LCD całego problemu, czyli wyświetlacz LCD górnego i dolnego mianownika.,

ponieważ wyświetlacz LCD 3y i 6y jest tylko \textbf{6Y}, pomnożymy teraz złożony licznik i mianownik przez ten wyświetlacz LCD. Po zrobieniu tego możemy oczekiwać, że problem zostanie zredukowany do jednego ułamka, który można uprościć jak zwykle.
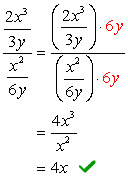
przykład 2: Uprość poniższy złożony ułamek.,
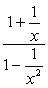
- używając metody 1
w tej metodzie chcemy utworzyć pojedynczy ułamek zarówno w liczniku, jak i mianowniku. Oczywiście ten problem wymagałby od nas zrobienia tego najpierw przed przeprowadzeniem sekcji.
Dodaj ułamki w liczniku, a odjmij ułamki w mianowniku.,
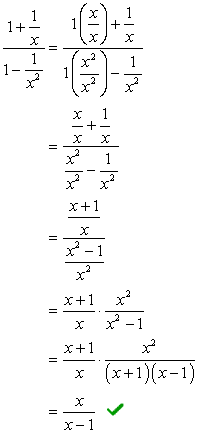
- używając metody 2
patrząc na mianowniki \large{X} i \large{X^2}, jego wyświetlacz LCD musi być \large{x^2} pomnóż górę i dół przez ten LCD.
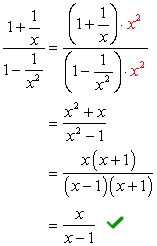
przykład 3: Uprość poniższy złożony ułamek.,
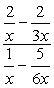
- używając metody 1
Utwórz pojedyncze ułamki zarówno w liczniku, jak i mianowniku, a następnie podziel ułamki.
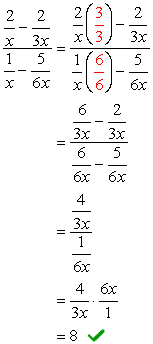
- używając metody 2
ogólny wyświetlacz LCD mianowników to \color{red}6x. użyj tego, aby pomnożyć przez górne i dolne wyrażenia.,
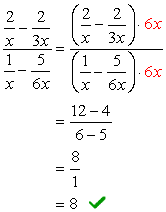
przykład 4: Uprość poniższy złożony ułamek.
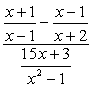
w przypadku tego problemu użyjemy tylko metody 1.
problem wymaga zastosowania metody foliowej (mnożenie dwóch dwumianów) oraz prostej faktoryzacji trójmianu. Na początku może to wyglądać nieco onieśmielająco, jednak jeśli zwracasz uwagę na szczegóły, gwarantuję ci, że nie jest tak źle.,
Jeśli zaobserwujemy, to mianownik złożony jest już w takiej postaci, jakiej chcemy-o jednym symbolu ułamkowym. Oznacza to, że musimy trochę popracować nad licznikiem złożonym. Naszym następnym krokiem będzie przekształcenie licznika złożonego w” prosty ” lub pojedynczy ułamek.
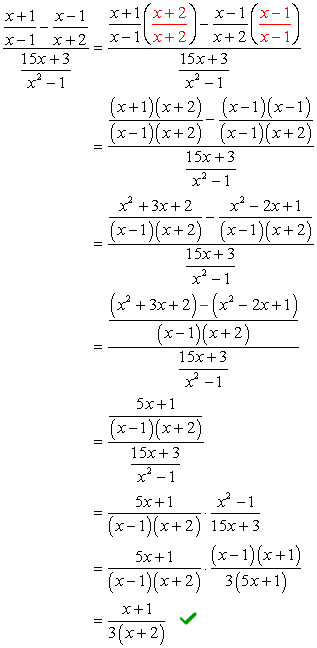
przykład 5: Uprość poniższy złożony ułamek.
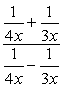
w przypadku tego problemu użyjemy tylko metody 2.,
zauważ, że LCD wszystkich mianowników jest po prostu \color{red}12x. Użyj tego jako wspólnego mnożnika zarówno dla wyrażenia górnego, jak i dolnego.
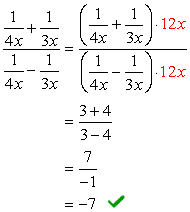
ćwicz z arkuszami roboczymi
ty może zainteresować Cię również:
mnożenie ułamków złożonych
dzielenie liczb zespolonych