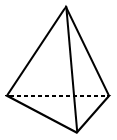
w geometrii wielościan jest zamkniętą przestrzenią, której twarze są wielokątami. Słowo polyhedron ma greckie pochodzenie, oznaczające wiele twarzy. Poniżej przedstawiono kilka przykładów polihedry.
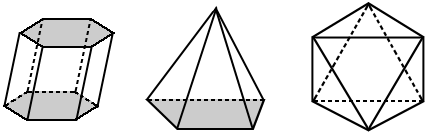
charakterystyka wielościanu
wielokąty, które tworzą wielościan, nazywane są twarzami. Segmenty linii utworzone przez dwie przecinające się powierzchnie nazywane są krawędziami. Wierzchołki są punktami, w których spotykają się trzy lub więcej krawędzi.,
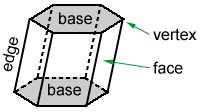
sześciokątny pryzmat powyżej jest wielościanem, który ma 6 bocznych powierzchni, które są równoległobokami i 2 powierzchnie na górze i na dole, zwane podstawami, które są sześciokątami.
twierdzenie Eulera
twierdzenie Eulera pokazuje zależność między liczbą powierzchni, wierzchołków i krawędzi wielościanu., Oznacza to, że suma powierzchni i wierzchołków minus liczba krawędzi jest zawsze równa dwóm:
F + V-E = 2
gdzie F to liczba powierzchni, V to liczba wierzchołków, A E to liczba krawędzi wielościanu.
przykład:
dla pryzmatu sześciokątnego pokazanego powyżej, F = 8 (sześć bocznych powierzchni + dwie podstawy), V = 12 i E = 18:
8 + 12 – 18 = 2
klasyfikacje polyhedry
Polyhedry można sklasyfikować na wiele sposobów. Na przykład mogą być klasyfikowane jako regularne i nieregularne wielościany., Wielościan regularny jest wielościanem, którego twarze są przystającymi wielokątami regularnymi; każdy wielościan, który nie spełnia tych warunków, jest uważany za nieregularny.
Polihedry można również klasyfikować jako wypukłe i wklęsłe. Wklęsły wielościan ma co najmniej jedną twarz, która jest wklęsłym wielokątem. Wielościan, który nie jest wklęsły, jest wypukły. Polihedra może być również klasyfikowana na podstawie liczby twarzy, które ma. Na przykład czworościan ma 4 twarze, pięciościan ma 5 twarzy, a sześciościan ma 6 twarzy.,
poniżej znajduje się lista terminów często używanych do opisania polihedry na podstawie ich cech.
pryzmaty
pryzmaty są wielościanami, które mają dwie przystające powierzchnie, zwane podstawami, leżące w równoległych płaszczyznach. Pryzmat jest zwykle nazywany przez kształt jego wielokątnych podstaw. Powierzchnie boczne (boki, które nie są podstawami) to równoległoboki, prostokąty lub kwadraty.,
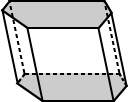
| pryzmat regularny | pryzmat nieregularny | 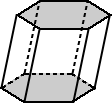 |
 |
|---|---|---|
| podstawy dla regularnego sześciokątnego pryzmatu powyżej mają podstawy, które są regularnymi sześciokątami. | podstawy pryzmatu sześciokątnego powyżej są sześciokątnymi nieregularnymi. |
piramidy
piramidy są polihedrą, która ma wielokąt jako podstawę i trójkąty jako wszystkie inne twarze.Nazwa piramidy pochodzi również od kształtu jej wielokątnej podstawy.,
| Piramida regularna | Piramida Nieregularna | 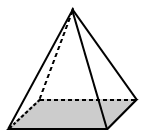 |
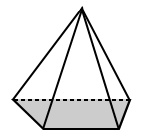 |
podstawa kwadratowej piramidy powyżej ma podstawę, która jest kwadratem (regularnym wielokątem). | podstawą powyższej piramidy trapezowej jest trapez o nierównych bokach (czyli jest to wielokąt nieregularny). |
|---|
regularna wielościan
regularna wielościan to wielościan, którego twarze są przystającymi, regularnymi wielokątami., Regularny wielościan jest nazwany na podstawie jego liczby twarzy. Istnieje tylko pięć polihedrów, które są regularnymi polihedrami; są one określane jako platoniczne ciała stałe.
pięć brył platonicznych
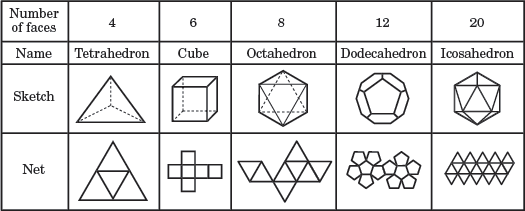
na powyższym diagramie każda zwykła polihedra jest nazwana na podstawie liczby powierzchni. Siatka pod każdym szkicem pokazuje obraz 2D wszystkich twarzy wielościanu.
Większość pryzmatów regularnych zwykle nie jest uważana za zwykłe polihedry., Sześcian jest jedynym regularnym pryzmatem, który można również zaklasyfikować jako regularny wielościan.
podobnie zwykły czworościan jest jedyną regularną piramidą, która jest również regularnym wielościanem.