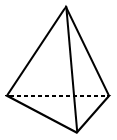
In der Geometrie ist ein Polyeder eine geschlossene Raumfigur, deren Flächen Polygone sind. Das Wort Polyeder hat griechischen Ursprung und bedeutet viele Gesichter. Im Folgenden sind einige Beispiele für Polyeder aufgeführt.
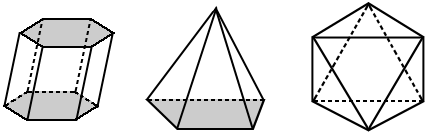
Eigenschaften eines Polyeders
Die Polygone, die ein Polyeder bilden, werden Gesichter genannt. Die Liniensegmente, die durch zwei sich kreuzende Flächen erzeugt werden, werden Kanten genannt. Die Eckpunkte sind Punkte, an denen sich drei oder mehr Kanten treffen.,
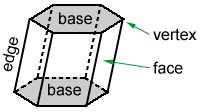
Das sechseckige Prisma oben ist ein Polyeder mit 6 Seitenflächen, die Parallelogramme sind, und 2 Flächen oben und unten, Basen genannt, das sind Sechsecke.
Eulers Satz
Eulers Satz zeigt eine Beziehung zwischen der Anzahl der Flächen, Eckpunkte und Kanten eines Polyeders., Es besagt, dass die Summe der Flächen und Eckpunkte abzüglich der Anzahl der Kanten immer gleich zwei ist:
F + V – E = 2
wobei F die Anzahl der Flächen, V die Anzahl der Eckpunkte und E die Anzahl der Kanten eines Polyeders ist.
Beispiel:
Für das oben gezeigte hexagonale Prisma F = 8 (sechs Seitenflächen + zwei Basen), V = 12 und E = 18:
8 + 12 – 18 = 2
Klassifikationen von Polyedern
Polyeder können auf viele Arten klassifiziert werden. Zum Beispiel können sie als reguläre und unregelmäßige Polyeder klassifiziert werden., Ein reguläres Polyeder ist ein Polyeder, dessen Flächen alle kongruenten regulären Polygone sind; Jedes Polyeder, das diese Bedingungen nicht erfüllt, gilt als unregelmäßig.
Polyeder können auch als konvex und konkav klassifiziert werden. Ein konkaves Polyeder hat mindestens eine Fläche, die ein konkaves Polygon ist. Ein Polyeder, das nicht konkav ist, ist konvex. Polyeder können auch anhand der Anzahl der Gesichter klassifiziert werden. Zum Beispiel hat ein Tetraeder 4 Gesichter, ein Pentaeder hat 5 Gesichter und ein Hexaeder hat 6 Gesichter.,
Das Folgende ist eine Liste von Begriffen, die häufig verwendet werden, um Polyeder basierend auf ihren Eigenschaften zu beschreiben.
Prismen
Prismen sind Polyeder mit zwei kongruenten Flächen, Basen genannt, die in parallelen Ebenen liegen. Ein Prisma wird typischerweise nach der Form seiner polygonalen Basen benannt. Die Seitenflächen (die Seiten, die keine Basen sind) sind Parallelogramme, Rechtecke oder Quadrate.,
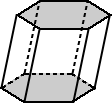
| Reguläres Prisma | Unregelmäßiges Prisma |
|---|---|
 |
|
| Die Basen für das reguläre sechseckige Prisma oben haben Basen, die regulär sind sechsecke. | Die Basen für das sechseckige Prisma oben sind unregelmäßig sechseckig. |
Pyramiden
Pyramiden sind Polyeder, die ein Polygon als Basis und Dreiecke als alle anderen Flächen haben.Eine Pyramide wird typischerweise auch nach der Form ihrer polygonalen Basis benannt.,
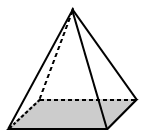
| Reguläre Pyramide | Unregelmäßige Pyramide |
|---|---|
 |
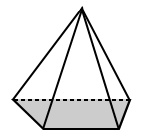 |
| Die Basis der quadratischen Pyramide oben hat eine Basis, die ein Quadrat ist (eine reguläre Pyramide polygon). | Die Basis für die obige trapezförmige Pyramide ist ein Trapez mit ungleichen Seiten (also ein unregelmäßiges Polygon). |
Reguläre Polyeder
Ein reguläres Polyeder ist ein Polyeder, dessen Flächen alle kongruente, reguläre Polygone sind., Ein reguläres Polyeder wird basierend auf seiner Anzahl von Flächen benannt. Es gibt nur fünf Polyeder, die regelmäßige Polyeder sind; Diese werden als platonische Feststoffe bezeichnet.
Die fünf platonischen Körper
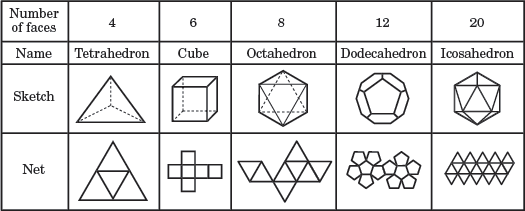
Im obigen Diagramm wird jedes reguläre Polyeder basierend auf seiner Anzahl von Flächen benannt. Das Netz unter jeder Skizze zeigt ein 2D-Bild aller Flächen des Polyeders.
Die meisten regulären Prismen gelten im Allgemeinen nicht als reguläre Polyeder., Ein Würfel ist das einzige reguläre Prisma, das auch als reguläres Polyeder klassifiziert werden kann.
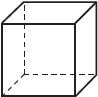
Ebenso ist ein reguläres Tetraeder die einzige reguläre Pyramide, die auch ein reguläres Polyeder ist.