această secțiune se uită la teorema binomială și Pascals triunghi.
Triunghiul lui Pascal
astfel încât (a + b)1 = a + b
(a + b)2 = a2 + 2ab + b2
(a + b)3 = a3 + 3a2b + 3b2a + b3
ar trebui să observați că coeficienții de (numerele înainte de a) a și b sunt:
1 1
1 2 1
1 3 3 1
Daca te-a continuat extinderea paranteze pentru puteri mai mari, v-ar găsi că secvența continuă:
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
etc
Această secvență este cunoscut sub numele de triunghiul lui Pascal., Fiecare dintre numere se găsește prin adăugarea celor două numere direct deasupra acestuia.
deci, 20 în ultima linie se găsește prin adăugarea împreună 10 și 10. Fiecare dintre 10s în linia de mai sus se găsesc prin adăugarea împreună a 6 și a 4.deci, este posibil să se extindă (A + b) la orice putere număr întreg prin cunoașterea triunghiul lui Pascal.
exemplu
găsiți (3 + x)3
puterea la care extindem paranteza este 3, deci ne uităm la a treia linie a triunghiului lui Pascal, care este 1 3 3 1.,deci, răspunsul este: 33 + 3 × (32 × x) + 3 × (x2 × 3) + x3(înlocuim a cu 3 și b cu x în extinderea (A + b) 3 de mai sus)
în general
este, desigur, adesea imposibil să scriem triunghiul lui Pascal de fiecare dată, când tot ce trebuie să știm sunt intrările de pe linia a noua. În mod clar, primul număr de pe linia A N-A este 1. Al doilea număr este n .al treilea număr este:
n(n – 1).
1 × 2
în general, numărul rth din linia nth este:
n! (care este nCr pe calculator)
r! (n-r)!
unde n!, înseamnă „n factorial” și este egal cu n × (n-1) × … × 2 × 1
nCr este, de asemenea, adesea scris ca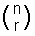
și se pronunță „n alege r”.
Teorema Binomială
Teorema Binomială prevede că, în cazul în care n este un număr întreg pozitiv:
-
(a + b)n = an + (nC1)o-1b + (nC2)o-2b2 + … + (nCn-1)abn-1 + bn
Exemplu
Expand (4 + 2x)6 în ordine crescătoare puterile lui x până la termenul în x3
Acest lucru înseamnă folosi teorema Binomială pentru a extinde termenii din paranteze, dar numai du-te la fel de mare ca x3.,
Deci, pentru a găsi răspunsul substitut 4 pentru a în teorema Binomială și 2x pentru b:
46 + (6C1)(45)(2x) + (6C2)(44)(2x)2 + (6C3)(43)(2x)3 + …
= 4096 + (6 ×1024 ×2x) + (15 ×256 ×4×2) + (20 ×64 ×8×3) + …
= 4096 + 12288x + 15360×2 + 10240×3 + …
Teorema Binomului (1 + x)n
versiunea anterioară a teorema binomului funcționează numai când n este un număr întreg pozitiv., If n is any fraction, the binomial theorem becomes:
| (1 + x)n | = | 1 | + | nx | + | n(n – 1)x2 | + | n(n – 1)(n – 2)x3 | + | … |
|
1! |
2! |
3!, |
FURNIZAREA |x| < 1
Rețineți că în timp ce seriile anterioare se oprește, asta merge pe pentru totdeauna.
exemplu
găsiți extinderea (5x + 2)1/2
trebuie să transformăm acest lucru astfel încât să pară (1 + x)1/2, deci să scoatem un factor de 2:
(5x + 2)1/2 = (2)1/2
acum, unde avem ” x ” în formula de mai sus, avem nevoie de 5x/2 și unde avem n, avem nevoie de½.,
= Ö2(1 + 5x/2)1/2
= Ö2
Amintiți-vă, acest lucru este valabil numai dacă -1 < 5x/2 < 1, cu alte cuvinte, -2/5 < x < 2/5
Utilizarea Parțială Fracțiuni
putem extinde mai multe expresii complicate, acum, folosind metoda de fracții parțiale acolo unde este cazul.
exemplu