introduktion
i detta experiment kommer du att observera de synliga våglängderna av ljus som produceras av en elektrisk urladdning i heliumgas, med hjälp av ett diffraktionsgitter. Från kunskap om våglängdsvärdena kommer du att kunna kalibrera diffraktionsgitterets radavstånd noggrant. När kalibrerad, gitter används för att mäta våglängden av ljus som produceras av atomväte. Genom att utföra en kurva som passar till dessa uppmätta våglängder kan du bestämma Rydbergkonstanten, en viktig fysisk konstant., Detta är ett experiment där noggrann teknik och mätning kommer att löna sig: du bör kunna bestämma Rydberg konstant till inom en procent eller bättre. Helium-och vätgaserna finns i urladdningsrör med lågt tryck som har metallelektroder i varje ände. När en hög spänning appliceras över de två elektroderna strömmar en elektrisk ström genom gasen. Högenergielektroner i den elektriska strömmen kolliderar med gasatomer och kan i processen ge inre energi till atomerna., Dessa upphetsade atomer kan sedan frigöra energi i form av elektromagnetisk strålning vid specifika våglängder. En del av denna elektromagnetiska strålning äri det synliga området.En schweizisk lärare vid namn Johann Balmer (1825 – 1898) studerade våglängderna av synligt ljus som avges av väteatomer. Han hittade en empirisk ekvation som exakt matchar värdenaav de observerade våglängderna.,
λ
= r

−
n2

, n = 3, 4, 5, 
här r är rydbergkonstanten 1, som har uppmätts exakt och visat sig ha värdet r = 10973731.5683 ± 0.0003 m–1. Variabeln n är ett heltal som är lika med eller större än 3. Serien av våglängder som härrör från n = 3, 4, 5,… kallas Balmer-serien.,1 Modern kvantteori av atomstruktur förutspår värdet av R i termer av andra grundläggande konstanter: C (ljusets hastighet), h (Plancks konstant), e (laddning av elektronen) och m (elektronens massa). Det experimentellt uppmätta värdet av R som anges ovan överensstämmer med den teoretiska förutsägelsen inom de kombinerade osäkerheterna för dessa andra grundläggande konstanter, vilket ger trovärdighet till teorin. Detta är ett bra exempel på var felanalys är nyckeln till att hjälpa oss att avgöra om en teori i fysik verkligen beskriver naturen.,Ett diffraktionsgaller kan användas för att observera de enskilda våglängderna av ljus som avges från urladdningsröret. Den gitter du kommer att använda har en linje eller spårtäthet på cirka 300 linjer / mm, sålunda är linjeavståndet d i storleksordningen 3 × 10-6 m. som ljus av våglängd λ Från urladdningsröret passerar genom gallret, diffraheras det genom en vinkel, θ, givet av gitterekvationen.
här m är ett heltal och kallas ordningen för diffraktionen., För gitter du kommer att använda, kommer dem = ± 1 och m = ± 2 Order vara lätt observerbar.Det experimentella arrangemanget som framgår av ovan visas i Figur 1. Du ser urladdningsröret ljus tittar genom diffraktionsgallret. Av till vänster och höger sida av röret bör du kunna se färgade bilder av urladdningsröret som visas ovanför och under mätaren stick. Figur 2 visar vyn genom gallret.,
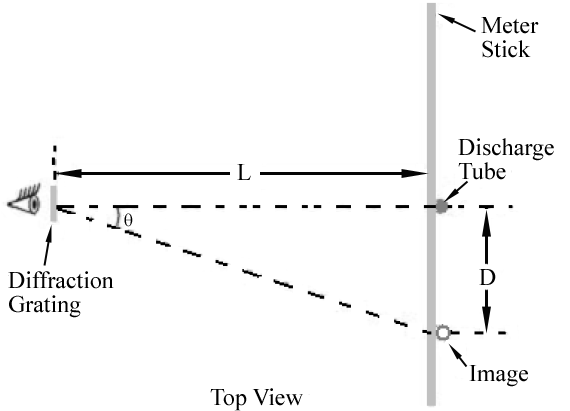
Figur 1
som visas i Figur 1 visas den första orderbilden för varje våglängd i en vinkel, θ, som uppfyller Eq. (2)
. Därför kommer olika våglängder att visas på olika platser längs mätaren. Vinkeln som motsvarar varje våglängd kan bestämmas genom mätning av D och L.
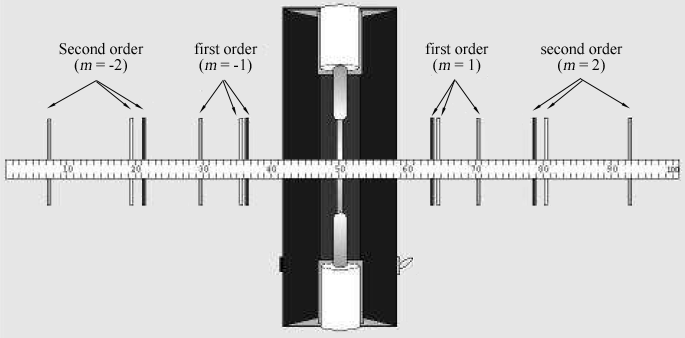
Figur 2: spektrallinjer som ses genom diffraktionsgitteret en meter från ett urladdningsrör.
Om λ Och θ är kända i Eq., (2)
, då d kan bestämmas. Du kommer att mäta θ för sju kända våglängder i helium. En kurvpassning gör det möjligt för dig att exakt bestämma gitteravståndet d.i den andra delen av labbet kommer du att använda detta värde av d för att noggrant mäta våglängder i väte.
procedur
Var extremt försiktig kring strömförsörjningen till utloppsröret. Den producerar 5000 volt med tillräcklig ström för att vara farlig. Rör inte vid matelektroderna eller röret när tillförseln är påslagen., Stäng av strömförsörjningen vid byte av urladdningsrör. Eftersom området blir mycket varmt under användning, undvik att ta tag i mitten av rören.
Del 1: Heliumspektrum
Ställ in arrangemanget som visas i Figur 1. Se till att strömförsörjningen till urladdningsröret är urkopplad och avstängd. Sätt i ett heliumgasrör i elektrodhållarna. (Rören är bräckliga; vänligen hantera dem med försiktighet.) Röret ska vara rakt upp och ner och placeras nära 50 cm-märket på mätaren.,
koppla in och slå på strömförsörjningen. Urladdningsröret ska omedelbart tändas. Om det inte gör det, be dig instruktör för hjälp. En labbpartner bör titta igenom diffraktionsgitteret medan den andra partnern arbetar på motsatt sida av mätarstickan och tar avläsningar.
den person som tittar genom diffraktionsgitteret ska se vänster och höger om urladdningsröret för att lokalisera diffraktionsbilderna. Leta reda på den första ordningen
och andra ordningen
bilder., Om det behövs, rotera gallret så att bilderna visas strax ovanför och under mätaren fastnar på samma sätt som urladdningsröret själv gör.
Tabell 1 visar våglängderna för sju av de ljusaste synliga linjerna i heliumspektrumet i storleksordningen kortast till längsta våglängd. Bilderna för varje diffraktionsordning visas i samma ordning, med den minsta våglängden i minsta vinkel. Matcha upp bilderna med de våglängder som anges. Titta genom gallret till höger, lokalisera positionen för den första bilden längs mätaren., Labbpartnern som tittar genom gallret bör instruera den andra labbpartnern att placera en liten pekare (t.ex. en penna) längs mätaren tills pekaren är i linje med bilden som mäts. Partnern med pekaren läser sedan positionen längs mätaren. Använd en låg wattal läslampa om det behövs för att läsa mätaren stick. Registrera positionen XR för var och en av heliumlinjerna i Tabell 1.
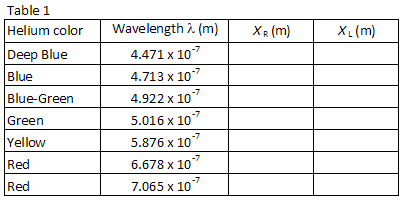
upprepa processen för de sju bilder som visas till vänster om urladdningsröret., Registrera positionen XL för varje bild i Tabell 1.
del 2: Vätgaspektrum
Stäng av och koppla ur strömförsörjningen och låt urladdningsröret svalna i flera minuter. (Varning: röret blir mycket varmt när du först stänger av strömmen.) Ta bort heliumröret och byt ut det med väteröret. Placera strömförsörjningen igen med väteröret i 50 cm-läget längs mätaren.
tre lätt observerade färger i väte anges i Tabell 2., Matcha färgerna med bilderna som ses genom diffraktionsgitteret. Spela in positionerna XR och XL för de första ordningsbilderna i Tabell 2.
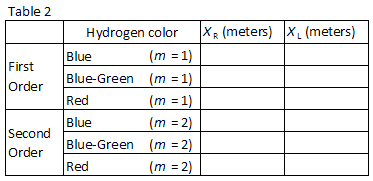
utan att störa mätaren stick eller diffraktionsgaller, noggrant mäta avståndet L i Figur 1 med hjälp av en metrisk måttband. Inkludera osäkerheten i ditt inspelade värde.,
analys
Gitteravstånd D
för varje heliumvåglängd, beräkna det genomsnittliga avståndet mellan urladdningsröret och de första orderbilderna med hjälp av följande ekvation.
XR − XL
beräknar också
d
l
, θ,
och sin θ för varje våglängd. Spela in dina beräkningar i tabell 3.
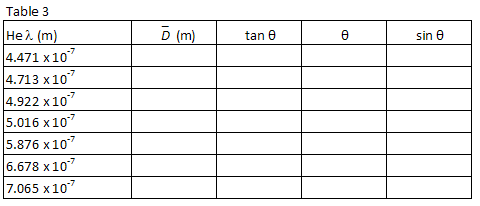
Plot λ vs., sin θ och, med en minst kvadrerad linjär passform, hitta lutningen. Från grafens lutning, hitta din bästa uppskattning för gitteravståndet, d, i meter och det uppskattade felet i d.
Rydberg Constant
efter samma procedur som används i steg 1 ovan, hitta sin θ för var och en av de vätevåglängder du observerade och registrera dem i Tabell 4.
använder värdet för gitteravståndet som finns i steg 2 ovan och gitterekvationen, Eq., (2)
, beräkna våglängden, i meter, av de tre vätelinjer du observerade och recordthose i Tabell 4.
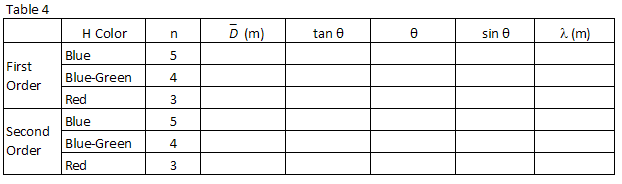
utför en minst kvadratisk linjär anpassning till dina data.
Eq. (1)
λ
= R

−
N2

, n = 3, 4, 5, 
kan skrivas om i följande form.,
λ
= R

no2
−
n2

jämför detta formulär med din kurvpassningsekvation för att hitta värden för konstanterna R och No. Fromthe error in the slope given by the curve fit, hitta osäkerheten för R.
diskussion
sammanfatta dina resultat för värdet av gitteravstånd och Rydbergkonstanten (både deras värden och deras osäkerheter)., Jämför kvantitativt ditt värde för Rydbergkonstanten med det accepterade värdet R = 10973732 m–1.