Wenn ein“ normaler “ Bruch Brüche entweder im Zähler oder Nenner oder in beiden enthält, betrachten wir ihn als komplexen Bruch. Diese Art von Fraktion wird auch als Verbundfraktion bezeichnet.
Es gibt zwei Methoden, solche Art von Bruch zu vereinfachen.
Method 1
wichtige Schritte:
- Erstellen Sie einen einzelnen Bruch im Zähler und Nenner.,
- Wenden Sie die Teilungsregel von Brüchen an, indem Sie den Zähler mit dem Kehrwert oder der Umkehrung des Nenners multiplizieren.
- Vereinfachen Sie bei Bedarf.
Methode 2
Wichtige Schritte:
- Finden Sie den kleinsten gemeinsamen Nenner (LCD) aller Nenner in den komplexen Brüchen.
- Multiplizieren Sie diese ZAHL mit dem Zähler und Nenner des komplexen Bruchs.
- Vereinfachen, falls erforderlich.,
Nachdem Sie einige Beispiele durchgegangen haben, sollten Sie feststellen, dass Methode 2 viel besser ist als Methode 1, da fast immer weniger Schritte erforderlich sind, um zur endgültigen Antwort zu gelangen.
Beispiele für die Vereinfachung komplexer Brüche
Beispiel 1: Vereinfachen Sie den folgenden komplexen Bruch.
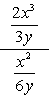
- Mit Methode 1
Sowohl der Zähler als auch der Nenner der komplexen Fraktion werden bereits als einzelne Brüche ausgedrückt. Das ist großartig!,

Der nächste Schritt besteht darin, die Divisionsregel anzuwenden, indem der Zähler mit dem Kehrwert des Nenners multipliziert wird. Beenden Sie, indem Sie allgemeine Faktoren aufheben, um die endgültige Antwort zu erhalten.
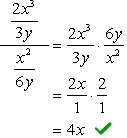
- Mit Methode 2
Finden Sie das LCD des gesamten Problems, dh das LCD des oberen und unteren Nenners.,

Da die LCD von 3y und 6y nur \textbf{6y} ist, multiplizieren wir jetzt den komplexen Zähler und Nenner mit diesem LCD. Danach können wir erwarten, dass das Problem auf einen einzigen Bruchteil reduziert wird, der wie üblich vereinfacht werden kann.
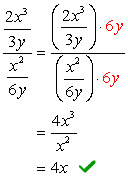
Beispiel 2: Vereinfachen Sie die komplexe Bruchteil unten.,
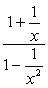
- Mit Methode 1
Bei dieser Methode möchten wir einen einzelnen Bruch sowohl im Zähler als auch im Nenner erstellen. Offensichtlich würde dieses Problem erfordern, dass wir das zuerst tun, bevor wir die Division durchführen.
Addieren Sie die Brüche im Zähler und subtrahieren Sie die Brüche im Nenner.,
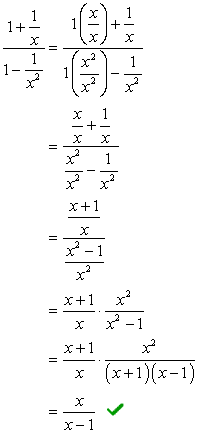
- Mit Methode 2
Wenn Sie die Nenner \large{x} und \large{x^2} betrachten, muss das LCD \large{x^2} Multiplizieren Sie oben und unten mit diesem LCD.
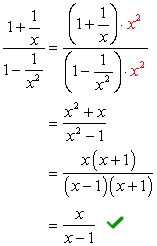
Beispiel 3: Vereinfachen Sie die komplexe Bruchteil unten.,
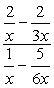
- Mit Methode 1
Erstellen Sie einzelne Brüche sowohl im Zähler als auch im Nenner.
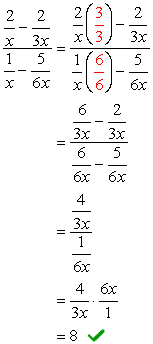
- Mit Methode 2
Die Gesamtgröße der Nenner ist \color{red}6x. Multiplizieren Sie damit durch die oberen und unteren Ausdrücke.,
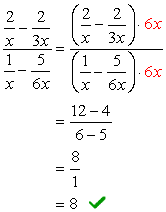
Beispiel 4: Vereinfachen Sie die komplexe Bruchteil unten.
Für dieses Problem verwenden wir nur Methode 1.
Das Problem erfordert, dass Sie die Folienmethode (Multiplikation zweier Binome) und eine einfache Faktorisierung von Trinomial anwenden. Es mag zunächst etwas einschüchternd aussehen; Wenn Sie jedoch auf Details achten, garantiere ich Ihnen, dass es nicht so schlimm ist.,
Wenn Sie beobachten, ist der komplexe Nenner bereits in der gewünschten Form – mit einem Bruchsymbol. Dies bedeutet, dass wir ein wenig an dem komplexen Zähler arbeiten müssen. Unser nächster Schritt wäre, den komplexen Zähler in einen „einfachen“ oder einzelnen Bruch umzuwandeln.
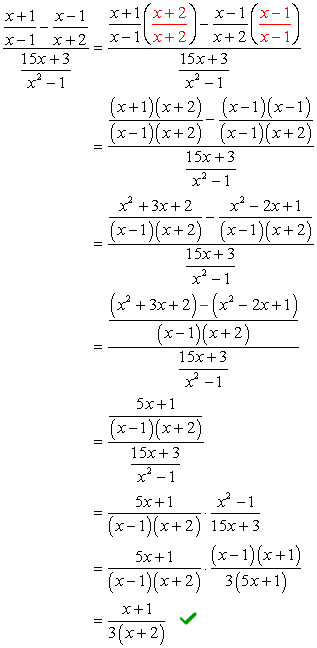
Beispiel 5: Vereinfachen Sie die komplexe Bruchteil unten.
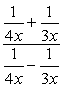
Für dieses Problem verwenden wir nur Methode 2.,
Beachten Sie, dass der LCD aller Nenner nur \color{red}12x. Verwenden Sie dies als gemeinsamen Multiplikator für den oberen und unteren Ausdruck.
Üben Sie mit Arbeitsblättern
Möglicherweise interessieren Sie sich auch für:
Multiplizieren komplexer Brüche
Komplexe Zahlen teilen