dette afsnit ser på Binomial Sætning og Pascals trekant.
Pascal ‘ s Trekant
så (a + b)1 = a + b
(a + b)2 = a2 + 2ab + b2
(a + b)3 = a3 + 3a2b + 3b2a + b3
Du bør bemærke, at koefficienterne i (tallene før) a og b er:
1 1
1 2 1
1 3 3 1
Hvis du fortsatte med at udvide beslag til højere magter, ville du opdage, at sekvensen fortsætter:
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
osv.
Denne sekvens er kendt som Pascal ‘ s trekant., Hvert af numrene findes ved at tilføje de to tal direkte over det.
så 20 i den sidste linje er fundet ved at tilføje sammen 10 og 10. Hver af 10 ‘ erne i linjen ovenfor findes ved at sammensætte en 6 og en 4.
så det er muligt at udvide (a + b) til en hel række magt ved at kende Pascal”s trekant.
eksempel
Find (3+.) 3
den effekt, som vi udvider beslaget til, er 3, så vi ser på den tredje linje i Pascals trekant, som er 1 3 3 1.,
Så svaret er: 33 + 3 × (32 × x) + 3 × (x2 × 3) + x3(vi er udskiftning af 3, og b af x i en udvidelse af (a + b)3 ovenfor)
Generelt
Det er naturligvis ofte upraktisk at skrive ud Pascal”s trekant, hver gang, når alle, at vi har brug for at vide, er de poster på den n ‘ te linje. Det er klart, at det første tal på den niende linje er 1. Det andet tal er n. det tredje tal er:
n(n – 1) .
1 2 2
generelt er det første nummer i den niende linje:
n! (som er nCr på din lommeregner)
r! (n – r)!
hvor n!, betyder ‘n factorial’ og er lig med n ((n-1) × … × 2 × 1
nCr skrives også ofte som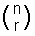 
og udtales”n vælg r”.
Den Binomiale Sætning
Den Binomiale Sætning hedder det, at hvis n er et positivt heltal, der er:
-
(a + b)n = an + (nC1)en-1b + (nC2)en-2b2 + … + (nCn-1)abn-1 + bn
Eksempel
Udvid (4 + 2x)6 i stigende potenser af x op til udtrykket i x3
Dette betyder at bruge den Binomiale sætning til at udvide udtrykkene i parenteser, men kun gå så højt som x3.,
Så til at finde de svar, vi erstatte 4 for et i den Binomiale sætning og 2x til b:
46 + (6C1)(45)(2x) + (6C2)(44)(2x)2 + (6C3)(43)(2x)3 + …
= 4096 + (6 ×1024 ×2x) + (15 ×256 ×4×2) + (20 ×64 ×8×3) + …
= 4096 + 12288x + 15360×2 + 10240×3 + …
Den Binomiale Sætning for (1 + x)n
Den tidligere version af den binomiale sætning virker kun, når n er et positivt heltal., If n is any fraction, the binomial theorem becomes:
| (1 + x)n | = | 1 | + | nx | + | n(n – 1)x2 | + | n(n – 1)(n – 2)x3 | + | … |
|
1! |
2! |
3!, |
GIVER |x| < 1
Bemærk, at mens de tidligere serier stopper, denne ene går på for evigt.
Eksempel
Find en udvidelse af (5x + 2)1/2
Vi er nødt til at ændre dette, så det ser ud som (1 + x)1/2, så lad os tage ud en faktor 2:
(5x + 2)1/2 = (2)1/2
Nu, hvor vi har ‘x’ i ovenstående formel, vi har brug for 5x/2, og hvor vi har n, vi har brug for½.,
= Ö2(1 + 5x/2)1/2
= Ö2
Husk, dette er kun gyldig, hvis -1 < 5x/2 < 1, med andre ord, -2/5 < x < 2/5
ved Hjælp af Delvis Fraktioner
Vi kan udvide mere komplicerede udtryk, nu, ved hjælp af den metode, der er delvis fraktioner, hvor det er relevant.
eksempel