introduktion
i dette eksperiment vil du observere de synlige bølgelængder af lys produceret af en elektrisk udladning i heliumgas ved hjælp af et diffraktionsgitter. Fra kendskab til bølgelængdeværdierne, duvil være i stand til nøjagtigt at kalibrere diffraktionsgitterets linjeafstand. Når den er kalibreret, bruges gitteret til at måle bølgelængden af lys produceret af atomart hydrogen. Ved at udføre en kurve, der passer til disse målte bølgelængder, kan du bestemme Rydberg-konstanten, en vigtig fysisk konstant., Dette er et eksperiment, hvor omhyggelig teknik og måling vil betale sig: du skal være i stand til at bestemme Rydberg-konstanten til inden for en procent eller bedre. Helium-og hydrogengasserne er indeholdt i lavtryksudladningsrør, der har metalelektroder i hver ende. Når en højspænding påføres over de to elektroder, strømmer en elektrisk strøm gennem gassen. Højenergielektroner i den elektriske strøm kolliderer med gasatomer og kan i processen give atomerne indre energi., Disse ophidsede atomer kan derefter frigive energi i form af elektromagnetisk stråling ved specifikke bølgelængder. Nogle af denne elektromagnetiske stråling eri det synlige område.En Sch .ei .isk skolelærer ved navn Johann Balmer (1825 – 1898) studerede bølgelængderne af synligt lys udsendt af hydrogenatomer. Han fandt en empirisk ligning, der nøjagtigt matcher værdierneaf de observerede bølgelængder.,
λ
= R

n2

, n = 3, 4, 5, 
Her R er Rydbergs konstant 1, der er nøje afstemt og fundet til at have den værdi, R = 10973731.5683 ± 0.0003 m–1. Variablen n er et heltal lig med eller større end 3. Rækken af bølgelængder, der er resultatet af n = 3, 4, 5,…, kaldes Balmer serien.,1 Moderne kvanteteori om atomstruktur forudsiger værdien af R med hensyn til andre grundlæggende konstanter: c (lysets hastighed), h (Plancks konstant), e (ladning af elektronen) og m (elektronens masse). Den eksperimentelt målte værdi af R givet ovenfor er enig med den teoretiske forudsigelse inden for de kombinerede usikkerheder af disse andre grundlæggende konstanter, hvilket giver troværdighed til teorien. Dette er et godt eksempel på, hvor fejlanalyse er nøglen til at hjælpe os med at afgøre, om en teori i fysik virkelig beskriver naturen.,Et diffraktionsgitter kan bruges til at observere de individuelle bølgelængder af lys, der udsendes fra udløbsrøret. Risten, du vil bruge, har en linje eller groove tæthed af ca 300 linjer/mm, således linjeafstanden d er på rækkefølgen af 3 × 10-6 m. Som lys af bølgelængden λ af decharge rør passerer gennem risten, det er diffracted gennem en vinkel, θ, i betragtning af risten ligning.
her er m et heltal og kaldes rækkefølgen af diffraktionen., For gitteret vil du bruge, dem = 1 1 og M = 2 2 ordrer vil være let observerbare.Forsøgsarrangementet set ovenfra er vist i Figur 1. Du ser udladningsrørets lys kigge gennem diffraktionsgitteret. Fra til venstre og højre side af røret skal du være i stand til at se farvede billeder af udløbsrøret, der vises over og under målepinden. Figur 2 viser udsigten set gennem gitteret.,
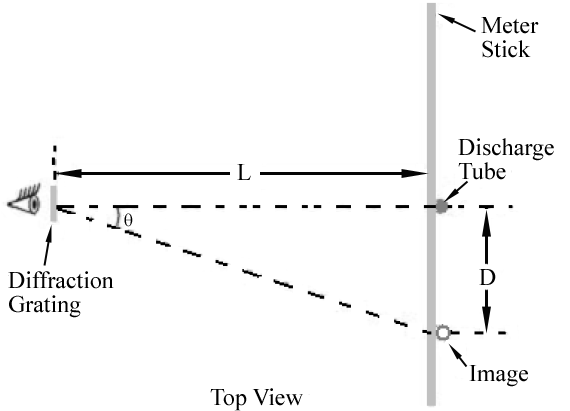
Figur 1
, Som vist i Figur 1, er den første ordre billede for hver bølgelængde vil blive vist i en vinkel, θ, der opfylder Eq. (2)
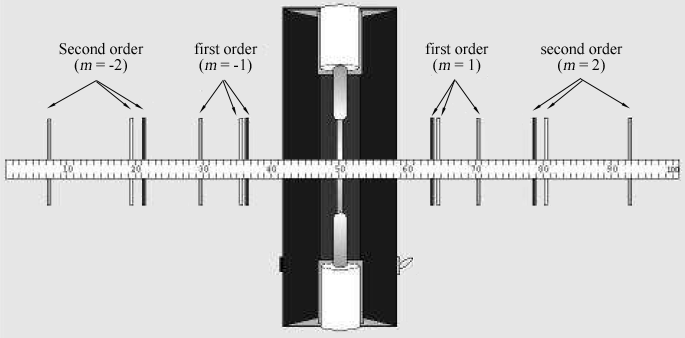
Figur 2: Spektrale linjer set gennem diffraktionsgitteret en meter fra et afløbsrør.
Hvis λ Og and er kendt i E.., (2)
Procedure
Brug ekstrem forsigtighed omkring udløbsrørets strømforsyning. Det producerer 5000 volt med tilstrækkelig strøm til at være farlig. Rør ikke ved forsyningselektroderne eller røret, mens forsyningen er tændt., Sluk for strømforsyningen, når du skifter udløbsrør. Da området bliver meget varmt under brug, skal du undgå at gribe fat i midten af rørene.
Del 1: Heliumspektrum
Indstil arrangementet vist i Figur 1. Sørg for, at udløbsrørets strømforsyning er frakoblet og slukket. Indsæt et heliumgasrør i elektrodeholderne. (Rørene er skrøbelige; behandl dem med omhu.) Røret skal være lige op og ned og placeret i nærheden af 50 cm mærket på målerpinden.,
Tilslut og tænd for strømforsyningen. Udløbsrøret skal straks lyse. Hvis det ikke gør det, bede dig instruktør om hjælp. En labpartner skal se gennem diffraktionsgitteret, mens den anden partner arbejder på den modsatte side af målepinden, der tager aflæsninger.
den person, der kigger gennem diffraktionsgitteret, skal se til venstre og højre for udløbsrøret for at finde diffraktionsbillederne. Find den første rækkefølge
og anden rækkefølge
billeder., Drej om nødvendigt gitteret, så billederne vises lige over og under målepinden på samme måde som udløbsrøret selv gør.
tabel 1 viser bølgelængderne for syv af de lyseste synlige linjer i heliumspektret i rækkefølgen af korteste til længste bølgelængde. Billederne for hver diffraktionsrækkefølge vises i samme rækkefølge med den mindste bølgelængde i den mindste vinkel. Match op billederne med bølgelængderne anført. Når du kigger gennem gitteret til højre, skal du finde placeringen af det første billede langs målerpinden., Laboratoriepartneren, der kigger gennem gitteret, skal instruere den anden laboratoriepartner om at placere en lille peger (f.eks. en blyant) langs målepinden, indtil markøren er i tråd med det billede, der måles. Partneren med markøren læser derefter positionen langs målepinden. Brug om nødvendigt en læselampe med lav effekt til at læse målepinden. Optag positionen positionr for hver af heliumlinjerne i tabel 1.
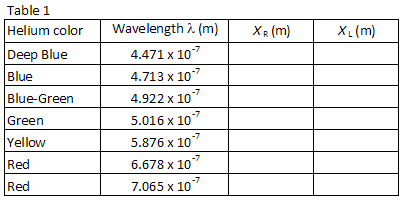
Gentag processen for de syv billeder, der vises til venstre for afløbsrør., Optag positionll for hvert billede i tabel 1.
Del 2: Hydrogenspektrum
Sluk og tag udladningsstrømforsyningen, og lad udløbsrøret afkøle i flere minutter. (Forsigtig: røret vil være meget varmt, når du først slukker for forsyningen.) Fjern heliumrøret og udskift det med brintrøret. Placer strømforsyningen igen med brintrøret i 50 cm-positionen langs målepinden.
tre let observerede farver i hydrogen er anført i tabel 2., Match farverne med billederne set gennem diffraktionsgitteret. Optag positionerne XR og andl for de første ordens billeder i tabel 2.
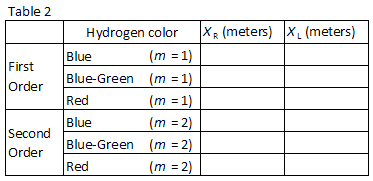
Uden at forstyrre måleren stick eller diffraction rist, omhyggeligt måle afstanden L i Figur 1 ved hjælp af en variabel, tape foranstaltning. Medtag usikkerheden i din registrerede værdi.,
analyse
gitterafstand d
for hver heliumbølgelængde beregnes den gennemsnitlige afstand mellem udløbsrøret og billederne i første rækkefølge ved hjælp af følgende ligning.
XR − XL
Også beregne
D
L
, θ,
og synd θ for hver bølgelængde. Optag dine beregninger i tabel 3.
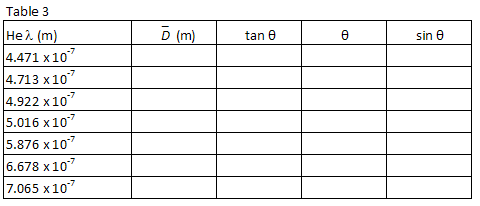
Plot λ vs., sin and og ved hjælp af en mindst kvadreret lineær pasform, finde hældningen. Fra hældningen af din graf med at finde dit bedste skøn for den rist afstand, d, i meter, og det anslås, fejl i d.
Rydbergs Konstant
Efter samme fremgangsmåde som i trin 1 ovenfor, find synd θ for hvert af brint bølgelængder, du har observeret og optage dem i Tabel 4.
ved hjælp af værdien for gitterafstanden fundet i trin 2 ovenfor og gitterligningen, e.., (2)
, Beregn bølgelængden i meter af de tre brintlinjer, du observerede, og registrer dem i tabel 4.
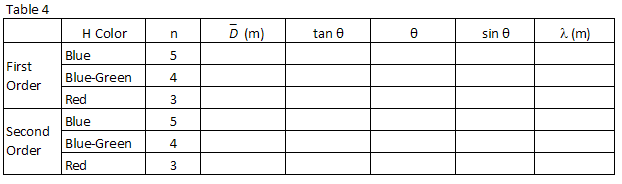
udfør en mindst firkantet lineær tilpasning til dine data.
e.. (1)
λ
= R

n2

, n = 3, 4, 5, 
kan skrives på følgende form.,
λ
= R

no2
n2

Undersøg denne formular for at din curve fit ligning til at finde værdier for konstanterne R og nej. Fromfejlen i hældningen givet af kurven passer, find usikkerheden for R.
Diskussion
Opsummer dine resultater for værdien af gitterafstand og Rydberg-konstanten (både deres værdier og deres usikkerheder)., Sammenlign kvantitativt din værdi for Rydberg-konstanten med den accepterede værdi R = 10973732 m–1.