Esta sección analiza el teorema Binomial y el Triángulo de Pascals.
Triángulo de Pascal
así que (a + b)1 = a + b
(A + b)2 = a2 + 2ab + b2
(A + b)3 = A3 + 3a2b + 3b2a + b3
debe notar que los coeficientes de (los números anteriores) a y b son:
1 1
1 2 1
1 3 3 1
Si continúa expandiendo los corchetes para potencias superiores, usted encontraría que la secuencia continúa:
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
etc
Esta secuencia se conoce como triángulo de Pascal., Cada uno de los números se encuentra sumando los dos números directamente encima de él.
Así que el 20 en la última línea se encuentra sumando 10 y 10. Cada uno de los 10 en la línea anterior se encuentran sumando un 6 y un 4.
así que es posible expandir (a + b) a cualquier potencia de número entero conociendo el triángulo de Pascal.
ejemplo
Find (3 + x) 3
la potencia a la que estamos expandiendo el corchete es 3, Así que miramos la tercera línea del triángulo de Pascal, que es 1 3 3 1.,
así que la respuesta es: 33 + 3 × (32 × x) + 3 × (x2 × 3) + x3(estamos reemplazando a por 3 y b por x en la expansión de (A + B)3 anterior)
generalmente
es, por supuesto, a menudo poco práctico escribir el triángulo de Pascal cada vez, cuando todo lo que necesitamos saber son las entradas en la enésima línea. Claramente, el primer número en la enésima línea es 1. El segundo número es n. El tercer número es:
n(n – 1) .
1 × 2
en general, el número r en la enésima línea es:
n! (que es nCr en su calculadora)
r! (n-r)!
donde n!, significa ‘n factorial’ y es igual a n × (n-1) × … × 2 × 1
nCr también se escribe a menudo como 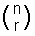 y se pronuncia «n choose r».
y se pronuncia «n choose r».
El teorema Binomial
El teorema Binomial establece que, donde n es un entero positivo:
-
(A + B)n = an + (nC1)an-1B + (nC2)an-2B2 + … + (nCn-1)abn-1 + bn
Ejemplo
Expand (4 + 2x)6 en potencias ascendentes de X hasta el término en X3
esto significa usar el teorema binomial para expandir los términos en los corchetes, pero solo ir tan alto como X3.,
así que para encontrar la respuesta sustituimos 4 por A en el teorema Binomial y 2x por b:
46 + (6C1)(45)(2x) + (6C2)(44)(2x)2 + (6C3)(43)(2x)3 + <
= 4096 + (6 ×1024 ×2x) + (15 ×256 ×4×2) + (20 ×64 ×8×3) + <
= 4096 + 12288x + 15360×2 + 10240×3 + the
El teorema binomial para (1 + x)n
la versión anterior del teorema binomial solo funciona cuando n es un entero positivo., If n is any fraction, the binomial theorem becomes:
| (1 + x)n | = | 1 | + | nx | + | n(n – 1)x2 | + | n(n – 1)(n – 2)x3 | + | … |
|
1! |
2! |
3!, |
PROPORCIONAR a |x| < 1
tenga en cuenta que mientras que la serie anterior se detiene, esto va para siempre.
Ejemplo
Encontrar la expansión de (5x + 2)1/2
Tenemos que transformar este modo parece que (1 + x)1/2, así que vamos a echar un factor de 2:
(5x + 2)1/2 = (2)1/2
Ahora, en donde hemos ‘x’ en la fórmula anterior, necesitamos 5x/2, y en donde tenemos n, necesitamos½.,
= Ö2(1 + 5x/2)1/2
= Ö2
Recuerde que esto sólo es válido si -1 < 5x/2 < 1, en otras palabras, -2/5 < x < 2/5
el Uso de Fracciones Parciales
podemos expandir expresiones más complicadas, ahora, utilizando el método de fracciones parciales cuando sea apropiado.
Ejemplo