Cette section examine le Théorème du Binôme et Pascals Triangle.
Triangle de Pascal
so (a + b)1 = a + b
(A + b)2 = a2 + 2ab + b2
(A + b)3 = a3 + 3a2b + 3b2a + b3
Vous devriez remarquer que les coefficients de (les nombres avant) a et b sont:
1 1
1 2 1
1 3 3 1
Si vous pour les puissances supérieures, vous trouverez que la séquence continue:
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
etc
Cette séquence est connue sous le nom de triangle de Pascal., Chacun des nombres est trouvé en additionnant les deux nombres directement au-dessus.
donc le 20 de la dernière ligne est trouvé en additionnant 10 et 10. Chacun des 10 dans la ligne ci-dessus sont trouvés en additionnant un 6 et un 4.
Il est donc possible d’étendre (a + b) à n’importe quelle puissance de nombre entier en connaissant le triangle de Pascal.
exemple
Find (3 + x)3
la puissance à laquelle nous étendons la parenthèse est 3, nous regardons donc la troisième ligne du triangle de Pascal, qui est 1 3 3 1.,
donc, la réponse est: 33 + 3 × (32 × x) + 3 × (x2 × 3) + x3(nous remplaçons a par 3 et b par x dans l’expansion de (a + b)3 ci-dessus)
généralement
Il est, bien sûr, souvent impraticable d’écrire le triangle de Pascal à chaque fois, quand tout ce que nous devons savoir sont les entrées sur la nième ligne. De toute évidence, le premier nombre sur la nième ligne est 1. Le deuxième nombre est N. Le troisième nombre est:
n (n-1).
1 × 2
en général, le rème nombre dans la nème ligne est:
n! (qui est nCr sur votre calculatrice)
r! (n-r)!
où n!, signifie « factorielle n » et est égale à n × (n-1) × … × 2 × 1
nCr est également souvent écrit que 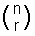 et se prononce « n choisir r”.
et se prononce « n choisir r”.
Le théorème Binomial
Le théorème Binomial indique que, où n est un entier positif:
-
(a + b)n = an + (nC1)an-1b + (nC2)an-2B2 + … + (nCn-1)abn-1 + bn
exemple
développez (4 + 2x)6 dans les puissances ascendantes de x pour le terme dans X3
cela signifie utiliser le théorème binomial pour étendre les Termes entre parenthèses, mais aller seulement aussi haut que X3.,
donc, pour trouver la réponse, nous substituons 4 pour a dans le théorème Binomial et 2x pour b:
46 + (6C1)(45)(2X) + (6C2)(44)(2x)2 + (6C3)(43)(2x)3 + <
= 4096 + (6 ×1024 ×2x) + (15 ×256 ×4×2) + (20 ×64 ×8×3) + br
= 4096 + 12288x + 15360×2 + 10240×3 + <
Le théorème binomial pour (1 + X)n
la version précédente du théorème binomial ne fonctionne que lorsque n est un entier positif., If n is any fraction, the binomial theorem becomes:
| (1 + x)n | = | 1 | + | nx | + | n(n – 1)x2 | + | n(n – 1)(n – 2)x3 | + | … |
|
1! |
2! |
3!, |
FOURNIR |x| < 1
Notez que, bien que la série s’arrête, celui-ci va à l’infini.
Exemple
Trouver l’expansion de (5x + 2)1/2
Nous avons besoin de transformer cette sorte qu’il ressemble (1 + x)1/2, donc permet de jeter un facteur de 2:
(5x + 2)1/2 = (2)1/2
Maintenant, où nous avons » x » dans la formule ci-dessus, nous avons besoin de 5x/2 et où nous avons n, nous avons besoin de½.,
= Ö2(1 + 5x/2)1/2
= Ö2
Rappelez-vous, ce n’est valable que si -1 < 5x/2 < 1, en d’autres termes, -2/5 < x < 2/5
l’Utilisation Partielle des Fractions
Nous pouvons développer des expressions plus complexes, maintenant, à l’aide de la méthode des fractions partielles, le cas échéant.
Exemple