Introduction
dans cette expérience, vous observerez les longueurs d’onde visibles de la lumière produite par une décharge électrique dans l’hélium gazeux, à l’aide d’un réseau de diffraction. À partir de la connaissance des valeurs de longueur d’onde, vous serez en mesure de calibrer avec précision l’espacement des lignes du réseau de diffraction. Une fois calibré, le réseau est utilisé pour mesurer la longueur d’onde de la lumière produite par l’hydrogène atomique. En effectuant une courbe adaptée à ces longueurs d’onde mesurées, vous pouvez déterminer la constante de Rydberg, une constante physique importante., Il s’agit d’une expérience dans laquelle une technique et une mesure soigneuses porteront leurs fruits: vous devriez être en mesure de déterminer la constante de Rydberg à un pour cent ou mieux. Les gaz d’hélium et d’hydrogène sont contenus dans des tubes à décharge basse pression qui ont des électrodes métalliques à chaque extrémité. Lorsqu’une haute tension est appliquée aux deux électrodes, un courant électrique traverse le gaz. Les électrons de haute énergie dans le courant électrique entrent en collision avec des atomes de gaz et, dans le processus, peuvent transmettre de l’énergie interne aux atomes., Ces atomes excités peuvent alors libérer de l’énergie sous forme de rayonnement électromagnétique à des longueurs d’onde spécifiques. Une partie de ce rayonnement électromagnétique estdans la gamme visible.Un instituteur Suisse nommé Johann Balmer (1825-1898) a étudié les longueurs d’onde de la lumière visible émise par les atomes d’hydrogène. Il a trouvé une équation empirique qui correspond avec précision aux valeursdes longueurs d’onde observées.,
λ
= R

−
n2

, n = 3, 4, 5, 
Ici, R est la constante de Rydberg 1, qui a été mesurée avec précision et constaté que la valeur de R = 10973731.5683 ± 0.0003 m–1. La variable n est tout entier égal ou supérieur à 3. La série de longueurs d’onde qui résultent de n = 3, 4, 5, …, s’appelle la série Balmer.,1 la théorie quantique moderne de la structure atomique prédit la valeur de R en termes d’autres constantes fondamentales: c (Vitesse de la lumière), h (constante de Planck), e (charge de l’électron) et m (masse de l’électron). La valeur expérimentalement mesurée de R donnée ci-dessus est en accord avec la prédiction théorique dans les incertitudes combinées de ces autres constantes fondamentales, donnant ainsi du crédit à la théorie. C’est un bon exemple où l’analyse des erreurs est essentielle pour nous aider à déterminer si une théorie en physique décrit vraiment la nature.,Un réseau de diffraction peut être utilisé pour observer les longueurs d’onde individuelles de la lumière émise par le tube à décharge. Le réseau que vous utiliserez a une densité de ligne ou de rainure d’environ 300 lignes/mm, donc l’espacement des lignes d est de l’ordre de 3 × 10-6 m. Comme la lumière de longueur d’onde λ du tube à décharge traverse le réseau, elle est diffractée à travers un angle, θ, donné par l’équation du réseau.
Ici m est un entier et est appelé l’ordre de la diffraction., Pour le réseau que vous utiliserez, les ordres = ± 1 et m = ± 2 seront facilement observables.La disposition expérimentale vue ci-dessus est illustrée à la Figure 1. Vous voyez la lumière du tube à décharge en regardant à travers le réseau de diffraction. Sur les côtés gauche et droit du tube, vous devriez pouvoir voir des images colorées du tube à décharge apparaissant au-dessus et au-dessous du bâton du compteur. La Figure 2 montre la vue vue à travers le réseau.,
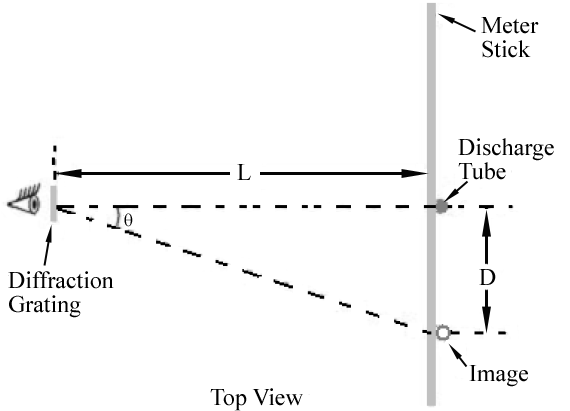
la Figure 1
Comme le montre la Figure 1, la première image d’ordre pour chaque longueur d’onde apparaît à un angle θ, satisfaisant Eq. (2)
. Par conséquent, différentes longueurs d’onde apparaîtront à différents endroits le long du bâton de compteur. L’angle correspondant à chaque longueur d’onde peut être déterminé en mesurant D et L.
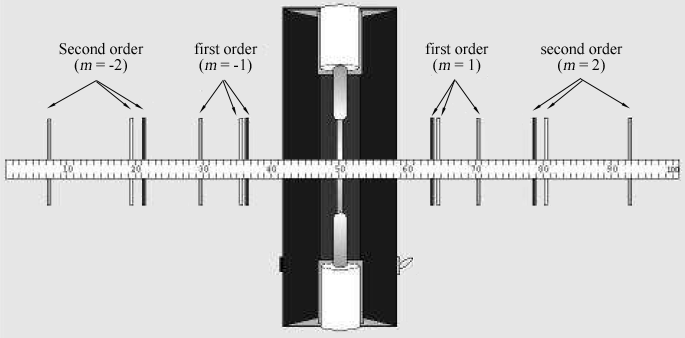
Figure 2: raies spectrales vues à travers le réseau de diffraction à un mètre d’un tube à décharge.
Si λ et θ sont connus dans l’éq., (2)
, alors d peut être déterminé. Vous mesurerez θ pour sept longueurs d’onde connues dans l’hélium. Un ajustement de courbe vous permettra ensuite de déterminer avec précision l’espacement du réseau D. dans la deuxième partie du laboratoire, vous utiliserez cette valeur de d pour mesurer avec précision les longueurs d’onde dans l’hydrogène.
Procédure
Utiliser une extrême prudence autour du tube de décharge électrique. Il produit 5000 volts avec un courant suffisant pour être dangereux. Ne touchez pas les électrodes d’alimentation ou le tube lorsque l’alimentation est allumée., Éteignez l’alimentation lors du Changement des tubes à décharge. Puisque la zone devient très chaude pendant l’utilisation, évitez de saisir le milieu des tubes.
Partie 1: Spectre de l’Hélium
configurer l’arrangement de la Figure 1. Assurez-vous que l’alimentation du tube à décharge est débranchée et éteinte. Insérez un tube d’hélium gazeux dans les porte-électrodes. (Les tubes sont fragiles; veuillez les manipuler avec soin.) Le tube doit être droit de haut en bas et positionné près de la marque de 50 cm sur le bâton du compteur.,
Branchez et allumez l’alimentation. Le tube à décharge doit immédiatement s’allumer. Si ce n’est pas le cas, demandez de l’aide à votre instructeur. Un partenaire de laboratoire devrait regarder à travers le réseau de diffraction tandis que l’autre partenaire travaille du côté opposé du bâton de compteur en prenant des lectures.
la personne qui regarde à travers le réseau de diffraction doit regarder à gauche et à droite du tube à décharge pour localiser les images de diffraction. Localisez les images du premier ordre
et du deuxième ordre
., Si nécessaire, faites pivoter le réseau de sorte que les images apparaissent juste au-dessus et au-dessous du bâton du compteur de la même manière que le tube à décharge lui-même.
le tableau 1 répertorie les longueurs d’onde de sept des raies visibles les plus brillantes du spectre de l’hélium dans l’ordre de la longueur d’onde la plus courte à la plus longue. Les images pour chaque ordre de diffraction apparaîtront dans le même ordre, avec la plus petite longueur d’onde au plus petit angle. Faire correspondre les images avec les longueurs d’onde répertoriés. En regardant à travers le réseau vers la droite, localisez la position de la première image le long du bâton du compteur., Le partenaire de laboratoire qui regarde à travers le réseau doit demander à l’autre partenaire de laboratoire de positionner un petit pointeur (par exemple, un crayon) le long du stick du compteur jusqu’à ce que le pointeur soit en ligne avec l’image mesurée. Le partenaire avec le pointeur lit ensuite la position le long du bâton du compteur. Utilisez une lampe de lecture à faible puissance si nécessaire pour lire le bâton du compteur. Enregistrer la position XR de chacune des raies d’hélium dans le tableau 1.
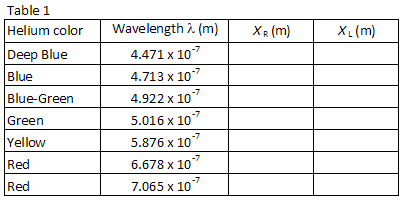
Répétez le processus pour les sept images qui apparaissent à la gauche du tube à décharge., Enregistrez la position XL de chaque image dans le tableau 1.
Partie 2: spectre de L’hydrogène
éteignez et débranchez l’alimentation de décharge et laissez le tube de décharge refroidir pendant plusieurs minutes. (Attention: le tube sera très chaud lorsque vous éteignez l’alimentation pour la première fois.) Retirez le tube d’hélium et remplacez-le par le tube d’hydrogène. Positionnez à nouveau l’alimentation électrique avec le tube d’hydrogène à la position 50 cm le long du bâton du compteur.
Trois facilement observer les couleurs de l’hydrogène sont répertoriés dans le Tableau 2., Faites correspondre les couleurs avec les images vues à travers le réseau de diffraction. Enregistrez les positions XR et XL des images de premier ordre dans le tableau 2.
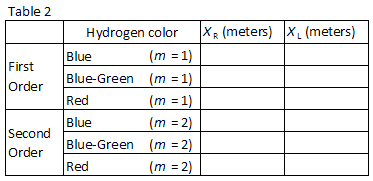
Sans perturber le mètre ou un réseau de diffraction, mesurez soigneusement la distance L de la Figure 1 à l’aide d’un ruban à mesurer métrique. Inclure l’incertitude dans votre valeur enregistrée.,
analyse
Espacement du réseau d
pour chaque longueur d’onde d’hélium, calculer la distance moyenne entre le tube à décharge et les images du premier ordre en utilisant l’équation suivante.
XR − XL
Aussi calculer
D
L
, θ,
et sin θ pour chaque longueur d’onde. Enregistrez vos calculs dans le tableau 3.
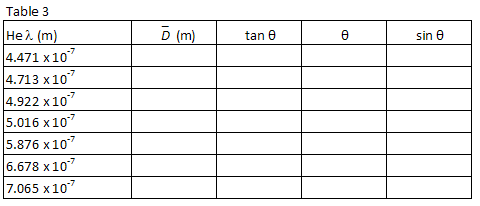
Plot λ vs, sin θ et, en utilisant un ajustement linéaire au moins carré, trouver la pente. À partir de la pente de votre graphique, Trouvez votre meilleure estimation pour l’espacement du réseau, d, en mètres et l’erreur estimée en D.
constante de Rydberg
en suivant la même procédure utilisée à l’étape 1 ci-dessus, recherchez sin θ pour chacune des longueurs d’onde de l’hydrogène
en utilisant la valeur de l’espacement de réseau trouvée à l’étape 2 ci-dessus et L’équation de réseau, Eq., (2)
, calculez la longueur d’onde, en mètres, des trois raies d’hydrogène que vous avez observées et enregistrez-les dans le tableau 4.
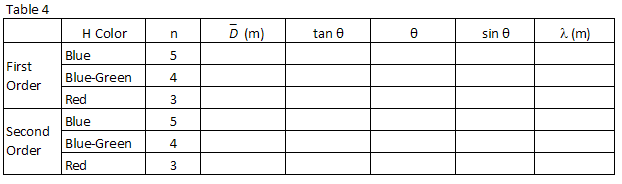
Effectuer un ajustement linéaire des moindres carrés à vos données.
Eq. (1)
λ
= R

−
n2

, n = 3, 4, 5, 
peut être réécrite sous la forme suivante.,
λ
= R

no2
−
n2

Comparer ce formulaire pour votre ajustement de la courbe d’équation pour trouver des valeurs pour les constantes R et non. A partir de l’erreur dans la pente donnée par l’ajustement de la courbe, trouvez L’incertitude pour R.
Discussion
résumez vos résultats pour la valeur de l’espacement du réseau et la constante de Rydberg (à la fois leurs valeurs et leurs incertitudes)., Comparez quantitativement votre valeur pour la constante de Rydberg avec la valeur acceptée R = 10973732 m–1.