Ez a szakasz a binomiális tételre és a Pascal-háromszögre néz.
Pascal-Háromszög
tehát (a + b)1 = a + b
(a + b)2 = a2 + 2ab + b2
(a + b)3 = a3 + 3a2b + 3b2a + b3
Meg kell jegyeznünk, hogy az együtthatók (a számok előtt), illetve a b a következők:
1 1
1 2 1
1 3 3 1
Ha tovább bővül a zárójelben a magasabb hatalmak, akkor azt találjuk, hogy a sorozat folytatódik:
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
stb
Ez a sorozat ismert Pascal-háromszög., A számok mindegyikét úgy találja meg, hogy a két számot közvetlenül hozzáadja.
tehát az utolsó sorban a 20-at 10-es és 10-es összesítéssel találjuk meg. Mind a 10-es a fenti sorban találhatók összeadásával egy 6 és egy 4.
így lehetséges, hogy bővítse (a + b) bármely egész szám teljesítmény ismeretében Pascal háromszög.
példa
Find (3 + x) 3
az a teljesítmény, amelyre a tartót kiterjesztjük, 3, tehát megnézzük Pascal háromszögének harmadik sorát, amely 1 3 3 1.,
Tehát a válasz: 33 + 3 × (32 × x) + 3 × (x2 × 3) + x3(vagyunk cseréje 3 b x a bővítése (a + b), a fenti 3.)
Általában
Ez persze gyakran nem célravezető, hogy írjon ki Pascal”s háromszög minden egyes alkalommal, ha minden, amit tudnunk kell, hogy a bejegyzéseket az n-edik sort. Nyilvánvaló, hogy az n. sor első száma 1. A második szám n. a harmadik szám:
n (n – 1) .
1 × 2
általában az n. sorban az rth szám:
n! (ami nCr a számológépen)
r! (n – r)!
ahol n!, “n faktoriális” és egyenlő: n × (n-1) × … × 2 × 1
nCr is gyakran van írva, mint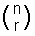 
és ejtik “n válassza r”.
A Binomiális Tétel
A Binomiális Tétel kimondja, hogy, ahol n pozitív egész szám:
-
(a + b)n = egy + (nC1)egy-1b + (nC2)egy-2b2 + … + (nCn-1)az abn-1 + bn
Példa
Expand (4 + 2x)6 növekvő ereje x a kifejezés x3
Ez azt jelenti, hogy használja a Binomiális tétel, hogy bontsa ki a feltételeket a zárójelben, de csak olyan magas, mint x3.,
Tehát, hogy megtalálja a választ, mi helyettesítő 4. a Binomiális tétel, illetve 2x b:
46 + (6C1)(45)(2x) + (6C2)(44)(2x)2 + (6C3)(43)(2x)3 + …
= 4096 + (6 ×1024 ×2x) + (15 ×256 ×4×2) + (20 ×64 ×8×3) + …
= 4096 + 12288x + 15360×2 + 10240×3 + …
A Binomiális Tétel az (1 + x)n
A korábbi változat a binomiális tétel csak akkor működik, ha n pozitív egész szám., If n is any fraction, the binomial theorem becomes:
| (1 + x)n | = | 1 | + | nx | + | n(n – 1)x2 | + | n(n – 1)(n – 2)x3 | + | … |
|
1! |
2! |
3!, |
PROVIDING |x| < 1
vegye figyelembe, hogy míg az előző sorozat leáll, ez örökre folytatódik.
Példa
keresse meg a bővítése (5x + 2)1/2
Úgy kell átalakítani, hogy ez úgy néz ki, mint (1 + x)1/2, így lehetővé teszi, hogy egy tényező 2:
(5x + 2)1/2 = (2)1/2
Most, ahol ” x ” a fenti képlet szükségünk van 5x/2, ahol n van szükségünk,½.,
= Ö2(1 + 5x/2)1/2
= Ö2
ne feledje, ez csak akkor érvényes, ha -1 < 5x/2 < 1, más szóval, -2/5 < x
div id=”dafa0b1668″>
2/5
részleges frakciók használata
bonyolultabb kifejezéseket bővíthetünk, most, adott esetben a részleges frakciók módszerével.
példa