w tej sekcji omówiono twierdzenie dwumianowe i trójkąt Pascala.
trójkąt Pascala
tak (a + b)1 = a + b
(A + b)2 = A2 + 2ab + b2
(A + b)3 = A3 + 3a2b + 3b2a + b3
należy zauważyć, że współczynniki (liczby przed) a i b są:
1 1
1 2 1
1 3 3 1
Jeśli nadal rozwijasz nawiasy dla potęg wyższych ciąg ten jest kontynuowany:
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
itd
ciąg ten jest znany jako trójkąt Pascala., Każda z liczb znajduje się przez dodanie dwóch liczb bezpośrednio nad nią.
Tak więc 20 w ostatnim wierszu znajduje się dodając razem 10 i 10. Każdy z 10s w linii powyżej znajdują się dodając razem 6 i 4.
Tak więc można rozszerzyć (a + b) na dowolną potęgę liczb całkowitych znając trójkąt Pascala.
przykład
Znajdź (3 + x)3
moc, którą rozszerzamy do 3, więc patrzymy na trzecią linię trójkąta Pascala, która wynosi 1 3 3 1.,
Tak więc odpowiedź brzmi: 33 + 3 × (32 × x) + 3 × (x2 × 3) + x3(zastępujemy a przez 3 i b przez x w rozszerzeniu (A + b)3 powyżej)
ogólnie
oczywiście często niepraktyczne jest wypisywanie trójkąta Pascala za każdym razem, gdy wszystko, co musimy wiedzieć, to wpisy w n-tej linii. Pierwsza liczba NA n-tej linii to 1. Druga liczba to N. trzecia liczba to:
N (n-1).
1 × 2
ogólnie rzecz biorąc, liczba rth w n-tej linii wynosi:
n! (czyli nCr na kalkulatorze)
r! (n-r)!
gdzie n!, oznacza ” n „i jest równa n × (n-1) × … × 2 × 1
nCr jest również często zapisywany jako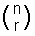 
I wymawia się „n wybierz r”.
twierdzenie dwumianowe
twierdzenie dwumianowe stwierdza, że gdzie n jest dodatnią liczbą całkowitą:
-
(a + b)n = an + (nC1)an-1B + (nC2)an-2B2 + … + (nCn-1)abn-1 + bn
przykład
rozwiń (4 + 2x)6 w potęgach rosnących x do wyrażenia w X3
oznacza to użycie twierdzenia dwumianowego do rozszerzenia terminów w nawiasach, ale tylko do X3.,
aby znaleźć odpowiedź zastępujemy 4 za a w twierdzeniu Dwumianowym i 2x za b:
46 + (6C1)(45)(2x) + (6C2)(44)(2x)2 + (6C3)(43)(2x)3 + …
= 4096 + (6 ×1024 ×2x) + (15 ×256 ×4×2) + (20 ×64 ×8×3) + …
= 4096 + 12288x + 15360×2 + 10240×3 + …
twierdzenie dwumianowe dla (1 + x)n
poprzednia wersja twierdzenia dwumianowego działa tylko wtedy, gdy n jest dodatnią liczbą całkowitą., If n is any fraction, the binomial theorem becomes:
| (1 + x)n | = | 1 | + | nx | + | n(n – 1)x2 | + | n(n – 1)(n – 2)x3 | + | … |
|
1! |
2! |
3!, |
zapewnienie| x/< 1
zauważ, że podczas gdy poprzednia seria się kończy, ta trwa wiecznie.
przykład
Znajdź rozszerzenie (5x + 2)1/2
musimy przekształcić to tak, aby wyglądało (1 + x) 1/2, więc wyjmijmy współczynnik 2:
(5x + 2)1/2 = (2)1/2
teraz, gdzie mamy ” x ” w powyższym wzorze, potrzebujemy 5x / 2, a gdzie mamy n, potrzebujemy½.,
= Ö2(1 + 5x/2)1/2
= Ö2
pamiętaj, że jest to ważne tylko wtedy, gdy -1 < 5x/2 < 1, innymi słowy, -2/5 < x < 2/5
używając ułamków częściowych
możemy teraz rozszerzać bardziej skomplikowane wyrażenia, używając metody ułamków częściowych, gdzie jest to właściwe.
przykład