This section looks at Binomial Theorem and Pascals Triangle.
Triângulo de Pascal
então, (a + b)1 = a + b
(a + b)2 = a2 + 2ab + b2
(a + b)3 = a3 + 3a2b + 3b2a + b3
Você deve observar que os coeficientes de (os números antes) a e b são:
1 1
1 2 1
1 3 3 1
Se você continuou expandindo os suportes para potências superiores, você teria que encontrar a sequência continua:
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
etc
Esta seqüência é conhecida como triângulo de Pascal., Cada um dos números é encontrado adicionando os dois números diretamente acima dele.
assim, os 20 na última linha são encontrados adicionando 10 e 10. Cada um dos 10s na linha acima são encontrados adicionando um 6 e um 4.
assim, é possível expandir (a + b) para qualquer potência de números inteiros, conhecendo o triângulo de Pascal.
exemplo
encontrar (3 + x)3
a potência a que estamos a expandir o suporte é 3, por isso olhamos para a terceira linha do triângulo de Pascal, que é 1 3 3 1.,
Então, a resposta é: 33 + 3 × (32 × x) + 3 × (2 × 3) + x3(estamos substituindo uma por 3 a e b por x na expansão de (a + b)3 acima).
Geral
é, claro, muitas vezes impraticável para escrever Pascal”s triângulo de cada vez, quando tudo o que precisamos saber são as entradas na enésima linha. Claramente, o primeiro número na linha n é 1. O segundo número é n. o terceiro número é:
n (n-1) .
1 × 2
em geral, o número rth na linha n É:
n! (que é nCr na sua calculadora)
R! (n-r)!em que n!, significa ‘n factorial’ e igual a n × (n-1) × … × 2 × 1
nCr também é muitas vezes escrito como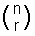 
e é pronunciado “n r”.
O Teorema Binomial
O Teorema Binomial estados que, onde n é um número inteiro positivo:
-
(a + b)n = an + (nC1)um-1b + (nC2)um-2b2 + … + (nCn-1)abn-1 + bn
Exemplo
Expand (4 + 2x)6, em ordem crescente de potências de x até o termo em x3
Isto significa utilizar o teorema Binomial para expandir os termos entre parênteses, mas apenas ir tão alto como x3.,
Então, para encontrar a resposta que o substituto de 4 em o teorema Binomial e 2x a b:
46 + (6C1)(45)(2x) + (6C2)(44)(2x)2 + (6C3)(43)(2x)3 + …
= 4096 + (6 ×1024 ×2x) + (15 ×256 ×4×2) + (20 ×64 ×8×3) + …
= 4096 + 12288x + 15360×2 + 10240×3 + …
O Teorema Binomial para (1 + x)n
A versão anterior do teorema binomial só funciona quando n é um número inteiro positivo., If n is any fraction, the binomial theorem becomes:
| (1 + x)n | = | 1 | + | nx | + | n(n – 1)x2 | + | n(n – 1)(n – 2)x3 | + | … |
|
1! |
2! |
3!, |
PROPORCIONANDO |x| < 1
Observe que, enquanto a série anterior pára, este vai para sempre.
Exemplo
Encontrar a expansão de (5x + 2)1/2
precisamos transformar esse então parece que (1 + x)1/2, então vamos tomar um fator de 2:
(5x + 2)1/2 = (2)1/2
Agora, onde temos ” x ” na fórmula acima, precisamos 5x/2, e onde temos n, precisamos½.,
= Ö2(1 + 5x/2)1/2
= Ö2
Lembre-se, isto só é válido se -1 < 5x/2 < 1, em outras palavras, -2/5 < x < 2/5
Usando Frações Parciais
podemos expandir mais complicado expressões, agora, usando o método das frações parciais, onde apropriado.
exemplo