det här avsnittet tittar på Binomial Theorem och Pascals Triangle.
Pascals triangel
Så (A + b)1 = a + b
(a + b)2 = a2 + 2AB + b2
(a + b)3 = a3 + 3a2b + 3b2a + b3
Du bör märka att koefficienterna för (siffrorna före) A och b är:
1 1
1 2 1
1 3 3 1
om du fortsätter att expandera parenteserna för högre befogenheter, du skulle upptäcka att sekvensen fortsätter:
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
etc
denna sekvens kallas Pascals triangel., Var och en av siffrorna hittas genom att lägga ihop de två siffrorna direkt ovanför den.
så 20 i den sista raden hittas genom att lägga ihop 10 och 10. Varje 10s i raden ovan finns genom att lägga ihop ett 6 och 4.
så det är möjligt att expandera (A + b) till en hel nummerkraft genom att känna Pascal”s triangel.
exempel
hitta (3 + x) 3
kraften som vi utökar konsolen till är 3, Så vi tittar på den tredje raden i Pascals triangel, vilket är 1 3 3 1.,
så svaret är: 33 + 3 × (32 × x) + 3 × (x2 × 3) + x3(vi ersätter a med 3 och B med x i expansionen av (A + b)3 ovan)
generellt
det är naturligtvis ofta opraktiskt att skriva ut Pascal”s triangel varje gång, när allt vi behöver veta är posterna på nth-linjen. Klart är det första numret på nth-linjen 1. Det andra numret är n. det tredje numret är:
n (n – 1) .
1 × 2
i allmänhet är RTH-numret i nth-linjen:
n! (vilket är nCr på din räknare)
r! (n – r)!
var n!, betyder ”n factorial” och är lika med n × (n-1) × … × 2 × 1
NCR skrivs också ofta som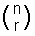 
och uttalas ”n choose r”.
Binomialteoremen
Binomialteoremen anger att, där n är ett positivt heltal:
-
(a + b)n = an + (NC1)an-1b + (NC2)an-2B2 + … + (NCN-1)abn-1 + bn
exempel
expandera (4 + 2x)6 i Binomialteoremen.stigande befogenheter x upp till termen i X3
det betyder att använda Binomialsatsen för att expandera termerna i parenteserna, men bara gå så högt som x3.,
så för att hitta svaret ersätter vi 4 för A i Binomialteoremen och 2x för b:
46 + (6C1)(45)(2x) + (6c2)(44)(2x)2 + (6C3)(43)(2x)3 + …
= 4096 + (6 ×1024 ×2x) + (15 ×256 ×4×2) + (20 ×64 ×8×3) + …
= 4096 + 12288x + 15360×2 + 10240×3 + …
Binomialteoremen för (1 + x)n
den tidigare versionen av binomialteoremen fungerar bara när n är ett positivt heltal., If n is any fraction, the binomial theorem becomes:
| (1 + x)n | = | 1 | + | nx | + | n(n – 1)x2 | + | n(n – 1)(n – 2)x3 | + | … |
|
1! |
2! |
3!, |
tillhandahålla| x/< 1
Observera att medan den tidigare serien stannar, fortsätter den för alltid.
exempel
hitta expansionen av (5x + 2)1/2
Vi måste omvandla detta så det ser ut (1 + x)1/2, så låt oss ta ut en faktor 2:
(5x + 2)1/2 = (2)1/2
nu, där vi har ” x ” i ovanstående formel, behöver vi 5x / 2 och där vi har n behöver vi½.,
= Ö2(1 + 5x/2)1/2
= Ö2
Kom ihåg att detta endast gäller om -1 < 5x/2 < 1, med andra ord -2/5 < x < 2/5
med hjälp av partiella fraktioner
vi kan expandera mer komplicerade uttryck, nu med hjälp av metoden för partiella fraktioner där det är lämpligt.
exempel